The Two Trains

I put this little question to a stationmaster, and his correct answer was so prompt that I am convinced there is no necessity to seek talented railway officials in America or elsewhere.
Two trains start at the same time, one from London to Liverpool, the other from Liverpool to London. If they arrive at their destinations one hour and four hours respectively after passing one another, how much faster is one train running than the other?

Solution

A Time Puzzle

How many minutes is it until six o'clock if fifty minutes ago it was four times as many minutes past three o'clock?

Solution

Concerning Tommy's Age

Tommy Smart was recently sent to a new school. On the first day of his arrival the teacher asked him his age, and this was his curious reply: "Well, you see, it is like this. At the time I was born—I forget the year—my only sister, Ann, happened to be just one-quarter the age of mother, and she is now one-third the age of father." "That's all very well," said the teacher, "but what I want is not the age of your sister Ann, but your own age." "I was just coming to that," Tommy answered; "I am just a quarter of mother's present age, and in four years' time I shall be a quarter the age of father. Isn't that funny?"
This was all the information that the teacher could get out of Tommy Smart. Could you have told, from these facts, what was his precise age? It is certainly a little puzzling.

Solution

Defective Observation

Our observation of little things is frequently defective, and our memories very liable to lapse. A certain judge recently remarked in a case that he had no recollection whatever of putting the wedding-ring on his wife's finger. Can you correctly answer these questions without having the coins in sight? On which side of a penny is the date given? Some people are so unobservant that, although they are handling the coin nearly every day of their lives, they are at a loss to answer this simple question. If I lay a penny flat on the table, how many other pennies can I place around it, every one also lying flat on the table, so that they all touch the first one? The geometrician will, of course, give the answer at once, and not need to make any experiment. He will also know that, since all circles are similar, the same answer will necessarily apply to any coin. The next question is a most interesting one to ask a company, each person writing down his answer on a slip of paper, so that no one shall be helped by the answers of others. What is the greatest number of three-penny-pieces that may be laid flat on the surface of a half-crown, so that no piece lies on another or overlaps the surface of the half-crown? It is amazing what a variety of different answers one gets to this question. Very few people will be found to give the correct number. Of course the answer must be given without looking at the coins.

Solution

The Bicycle Thief

Here is a little tangle that is perpetually cropping up in various guises. A cyclist bought a bicycle for £15 and gave in payment a cheque for £25. The seller went to a neighbouring shopkeeper and got him to change the cheque for him, and the cyclist, having received his £10 change, mounted the machine and disappeared. The cheque proved to be valueless, and the salesman was requested by his neighbour to refund the amount he had received. To do this, he was compelled to borrow the £25 from a friend, as the cyclist forgot to leave his address, and could not be found. Now, as the bicycle cost the salesman £11, how much money did he lose altogether?

Solution

The Market Women

A number of market women sold their various products at a certain price per pound (different in every case), and each received the same amount—2s. 2½d. What is the greatest number of women there could have been? The price per pound in every case must be such as could be paid in current money.

Solution

Indiscriminate Charity

A charitable gentleman, on his way home one night, was appealed to by three needy persons in succession for assistance. To the first person he gave one penny more than half the money he had in his pocket; to the second person he gave twopence more than half the money he then had in his pocket; and to the third person he handed over threepence more than half of what he had left. On entering his house he had only one penny in his pocket. Now, can you say exactly how much money that gentleman had on him when he started for home?

Solution

Who was First?

Anderson, Biggs, and Carpenter were staying together at a place by the seaside. One day they went out in a boat and were a mile at sea when a rifle was fired on shore in their direction. Why or by whom the shot was fired fortunately does not concern us, as no information on these points is obtainable, but from the facts I picked up we can get material for a curious little puzzle for the novice.
It seems that Anderson only heard the report of the gun, Biggs only saw the smoke, and Carpenter merely saw the bullet strike the water near them. Now, the question arises: Which of them first knew of the discharge of the rifle?

Solution

The Dovetailed Block

Here is a curious mechanical puzzle that was given to me some years ago, but I cannot say who first invented it. It consists of two solid blocks of wood securely dovetailed together. On the other two vertical sides that are not visible the appearance is precisely the same as on those shown. How were the pieces put together? When I published this little puzzle in a London newspaper I received (though they were unsolicited) quite a stack of models, in oak, in teak, in mahogany, rosewood, satinwood, elm, and deal; some half a foot in length, and others varying in size right down to a delicate little model about half an inch square. It seemed to create considerable interest.

Solution

The Siberian Dungeons

The above is a trustworthy plan of a certain Russian prison in Siberia. All the cells are numbered, and the prisoners are numbered the same as the cells they occupy. The prison diet is so fattening that these political prisoners are in perpetual fear lest, should their pardon arrive, they might not be able to squeeze themselves through the narrow doorways and get out. And of course it would be an unreasonable thing to ask any government to pull down the walls of a prison just to liberate the prisoners, however innocent they might be. Therefore these men take all the healthy exercise they can in order to retard their increasing obesity, and one of their recreations will serve to furnish us with the following puzzle.
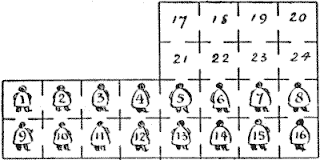
Show, in the fewest possible moves, how the sixteen men may form themselves into a magic square, so that the numbers on their backs shall add up the same in each of the four columns, four rows, and two diagonals without two prisoners having been at any time in the same cell together. I had better say, for the information of those who have not yet been made acquainted with these places, that it is a peculiarity of prisons that you are not allowed to go outside their walls. Any prisoner may go any distance that is possible in a single move.

Solution

Crossing the River Axe

Many years ago, in the days of the smuggler known as "Rob Roy of the West," a piratical band buried on the coast of South Devon a quantity of treasure which was, of course, abandoned by them in the usual inexplicable way. Some time afterwards its whereabouts was discovered by three countrymen, who visited the spot one night and divided the spoil between them, Giles taking treasure to the value of £800, Jasper £500 worth, and Timothy £300 worth. In returning they had to cross the river Axe at a point where they had left a small boat in readiness. Here, however, was a difficulty they had not anticipated. The boat would only carry two men, or one man and a sack, and they had so little confidence in one another that no person could be left alone on the land or in the boat with more than his share of the spoil, though two persons (being a check on each other) might be left with more than their shares. The puzzle is to show how they got over the river in the fewest possible crossings, taking their treasure with them. No tricks, such as ropes, "flying bridges," currents, swimming, or similar dodges, may be employed.

Solution

Puss in the Corner

This variation of the last puzzle is also played by two persons. One puts a counter on No. 6, and the other puts one on No. 55, and they play alternately by removing the counter to any other number in a line. If your opponent moves at any time on to one of the lines you occupy, or even crosses one of your lines, you immediately capture him and win. We will take an illustrative game.
A moves from 55 to 52; B moves from 6 to 13; A advances to 23; B goes to 15; A retreats to 26; B retreats to 13; A advances to 21; B retreats to 2; A advances to 7; B goes to 3; A moves to 6; B must now go to 4; A establishes himself at 11, and B must be captured next move because he is compelled to cross a line on which A stands. Play this over and you will understand the game directly. Now, the puzzle part of the game is this: Which player should win, and how many moves are necessary?

Solution

Card Triangles

Here you pick out the nine cards, ace to nine of diamonds, and arrange them in the form of a triangle, exactly as shown in the illustration, so that the pips add up the same on the three sides. In the example given it will be seen that they sum to 20 on each side, but the particular number is of no importance so long as it is the same on all three sides. The puzzle is to find out in just how many different ways this can be done.
If you simply turn the cards round so that one of the other two sides is nearest to you this will not count as different, for the order will be the same. Also, if you make the 4, 9, 5 change places with the 7, 3, 8, and at the same time exchange the 1 and the 6, it will not be different. But if you only change the 1 and the 6 it will be different, because the order round the triangle is not the same. This explanation will prevent any doubt arising as to the conditions.

Solution

The Barrel Puzzle

The men in the illustration are disputing over the liquid contents of a barrel. What the particular liquid is it is impossible to say, for we are unable to look into the barrel; so we will call it water. One man says that the barrel is more than half full, while the other insists that it is not half full. What is their easiest way of settling the point? It is not necessary to use stick, string, or implement of any kind for measuring. I give this merely as one of the simplest possible examples of the value of ordinary sagacity in the solving of puzzles. What are apparently very difficult problems may frequently be solved in a similarly easy manner if we only use a little common sense.

Solution

An Amazing Dilemma

In a game of chess between Mr. Black and Mr. White, Black was in difficulties, and as usual was obliged to catch a train. So he proposed that White should complete the game in his absence on condition that no moves whatever should be made for Black, but only with the White pieces. Mr. White accepted, but to his dismay found it utterly impossible to win the game under such conditions. Try as he would, he could not checkmate his opponent. On which square did Mr. Black leave his king? The other pieces are in their proper positions in the diagram. White may leave Black in check as often as he likes, for it makes no difference, as he can never arrive at a checkmate position.

Solution

The Kennal Puzzle

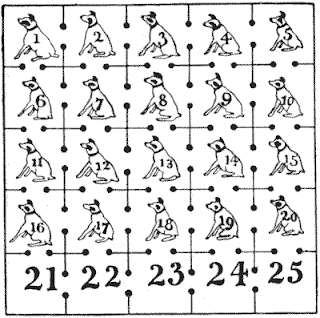A man has twenty-five dog kennels all communicating with each other by doorways, as shown in the illustration. He wishes to arrange his twenty dogs so that they shall form a knight's string from dog No. 1 to dog No. 20, the bottom row of five kennels to be left empty, as at present. This is to be done by moving one dog at a time into a vacant kennel. The dogs are well trained to obedience, and may be trusted to remain in the kennels in which they are placed, except that if two are placed in the same kennel together they will fight it out to the death. How is the puzzle to be solved in the fewest possible moves without two dogs ever being together?

Solution is here

St. George and the Dragon

Here is a little puzzle on a reduced chessboard of forty-nine squares. St. George wishes to kill the dragon. Killing dragons was a well-known pastime of his, and, being a knight, it was only natural that he should desire to perform the feat in a series of knight's moves. Can you show how, starting from that central square, he may visit once, and only once, every square of the board in a chain of chess knight's moves, and end by capturing the dragon on his last move? Of course a variety of different ways are open to him, so try to discover a route that forms some pretty design when you have marked each successive leap by a straight line from square to square.

Solution

The Lion and the Man

In a public place in Rome there once stood a prison divided into sixty-four cells, all open to the sky and all communicating with one another, as shown in the illustration. The sports that here took place were watched from a high tower. The favourite game was to place a Christian in one corner cell and a lion in the diagonally opposite corner and then leave them with all the inner doors open. The consequent effect was sometimes most laughable. On one occasion the man was given a sword. He was no coward, and was as anxious to find the lion as the lion undoubtedly was to find him.

The man visited every cell once and only once in the fewest possible straight lines until he reached the lion's cell. The lion, curiously enough, also visited every cell once and only once in the fewest possible straight lines until he finally reached the man's cell. They started together and went at the same speed; yet, although they occasionally got glimpses of one another, they never once met. The puzzle is to show the route that each happened to take.

Solution

The Southern Cross

In the above illustration we have five Planets and eighty-one Fixed Stars, five of the latter being hidden by the Planets. It will be found that every Star, with the exception of the ten that have a black spot in their centres, is in a straight line, vertically, horizontally, or diagonally, with at least one of the Planets. The puzzle is so to rearrange the Planets that all the Stars shall be in line with one or more of them.
In rearranging the Planets, each of the five may be moved once in a straight line, in either of the three directions mentioned. They will, of course, obscure five other Stars in place of those at present covered.

Solution

The Bachet's Square

One of the oldest card puzzles is by Claude Caspar Bachet de Méziriac, first published, I believe, in the 1624 edition of his work. Rearrange the sixteen court cards (including the aces) in a square so that in no row of four cards, horizontal, vertical, or diagonal, shall be found two cards of the same suit or the same value. This in itself is easy enough, but a point of the puzzle is to find in how many different ways this may be done. The eminent French mathematician A. Labosne, in his modern edition of Bachet, gives the answer incorrectly. And yet the puzzle is really quite easy. Any arrangement produces seven more by turning the square round and reflecting it in a mirror. These are counted as different by Bachet.

Note "row of four cards," so that the only diagonals we have here to consider are the two long ones

Solution

The Chessboard Sentence

I once set myself the amusing task of so dissecting an ordinary chessboard into letters of the alphabet that they would form a complete sentence. It will be seen from the illustration that the pieces assembled give the sentence, "CUT THY LIFE," with the stops between. The ideal sentence would, of course, have only one full stop, but that I did not succeed in obtaining.
The sentence is an appeal to the transgressor to cut himself adrift from the evil life he is living. Can you fit these pieces together to form a perfect chessboard?

Solution

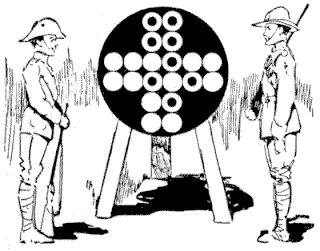
The Cross Target

In the illustration we have a somewhat curious target designed by an eccentric sharpshooter. His idea was that in order to score you must hit four circles in as many shots so that those four shots shall form a square. It will be seen by the results recorded on the target that two attempts have been successful. The first man hit the four circles at the top of the cross, and thus formed his square. The second man intended to hit the four in the bottom arm, but his second shot, on the left, went too high. This compelled him to complete his four in a different way than he intended. It will thus be seen that though it is immaterial which circle you hit at the first shot, the second shot may commit you to a definite procedure if you are to get your square. Now, the puzzle is to say in just how many different ways it is possible to form a square on the target with four shots.

Solution

The Mouse-Trap Puzzle

This is a modern version, with a difference, of an old puzzle of the same name. Number twenty-one cards, 1, 2, 3, etc., up to 21, and place them in a circle in the particular order shown in the illustration. These cards represent mice. You start from any card, calling that card "one," and count, "one, two, three," etc., in a clockwise direction, and when your count agrees with the number on the card, you have made a "catch," and you remove the card. Then start at the next card, calling that "one," and try again to make another "catch." And so on. Supposing you start at 18, calling that card "one," your first "catch" will be 19. Remove 19 and your next "catch" is 10. Remove 10 and your next "catch" is 1. Remove the 1, and if you count up to 21 (you must never go beyond), you cannot make another "catch." Now, the ideal is to "catch" all the twenty-one mice, but this is not here possible, and if it were it would merely require twenty-one different trials, at the most, to succeed. But the reader may make any two cards change places before he begins. Thus, you can change the 6 with the 2, or the 7 with the 11, or any other pair. This can be done in several ways so as to enable you to "catch" all the twenty-one mice, if you then start at the right place. You may never pass over a "catch"; you must always remove the card and start afresh.

Solution

The City Luncheons

Twelve men connected with a large firm in the City of London sit down to luncheon together every day in the same room. The tables are small ones that only accommodate two persons at the same time. Can you show how these twelve men may lunch together on eleven days in pairs, so that no two of them shall ever sit twice together? We will represent the men by the first twelve letters of the alphabet, and suppose the first day's pairing to be as follows—
(A B) (C D) (E F) (G H) (I J) (K L).
Then give any pairing you like for the next day, say—
(A C) (B D) (E G) (F H) (I K) (J L),
and so on, until you have completed your eleven lines, with no pair ever occurring twice. There are a good many different arrangements possible. Try to find one of them.

Solutions

The Motor-Car Tour

In the above diagram the circles represent towns and the lines good roads. In just how many different ways can a motorist, starting from London (marked with an L), make a tour of all these towns, visiting every town once, and only once, on a tour, and always coming back to London on the last ride? The exact reverse of any route is not counted as different.

Solution

The Fifteen Turnings

Here is another queer travelling puzzle, the solution of which calls for ingenuity. In this case the traveller starts from the black town and wishes to go as far as possible while making only fifteen turnings and never going along the same road twice. The towns are supposed to be a mile apart. Supposing, for example, that he went straight to A, then straight to B, then to C, D, E, and F, you will then find that he has travelled thirty-seven miles in five turnings. Now, how far can he go in fifteen turnings?



Solution

The Exchange Puzzle

Here is a rather entertaining little puzzle with moving counters. You only need twelve counters—six of one colour, marked A, C, E, G, I, and K, and the other six marked B, D, F, H, J, and L. You first place them on the diagram, as shown in the illustration, and the puzzle is to get them into regular alphabetical order, as follows:—

A B C D
E F G H
I J K L

The moves are made by exchanges of opposite colours standing on the same line. Thus, G and J may exchange places, or F and A, but you cannot exchange G and C, or F and D, because in one case they are both white and in the other case both black. Can you bring about the required arrangement in seventeen exchanges?

It cannot be done in fewer moves. The puzzle is really much easier than it looks, if properly attacked.

Solution

The Motor-Garage Puzzle

The difficulties of the proprietor of a motor garage are converted into a little pastime of a kind that has a peculiar fascination. All you need is to make a simple plan or diagram on a sheet of paper or cardboard and number eight counters, 1 to 8. Then a whole family can enter into an amusing competition to find the best possible solution of the difficulty.
The illustration represents the plan of a motor garage, with accommodation for twelve cars. But the premises are so inconveniently restricted that the proprietor is often caused considerable perplexity. Suppose, for example, that the eight cars numbered 1 to 8 are in the positions shown, how are they to be shifted in the quickest possible way so that 1, 2, 3, and 4 shall change places with 5, 6, 7, and 8—that is, with the numbers still running from left to right, as at present, but the top row exchanged with the bottom row? What are the fewest possible moves?
One car moves at a time, and any distance counts as one move. To prevent misunderstanding, the stopping-places are marked in squares, and only one car can be in a square at the same time.

Solution

The Six Frogs

The six educated frogs in the illustration are trained to reverse their order, so that their numbers shall read 6, 5, 4, 3, 2, 1, with the blank square in its present position. They can jump to the next square (if vacant) or leap over one frog to the next square beyond (if vacant), just as we move in the game of draughts, and can go backwards or forwards at pleasure. Can you show how they perform their feat in the fewest possible moves? It is quite easy, so when you have done it add a seventh frog to the right and try again. Then add more frogs until you are able to give the shortest solution for any number. For it can always be done, with that single vacant square, no matter how many frogs there are.

Solution

A new match Puzzle

In the illustration eighteen matches are shown arranged so that they enclose two spaces, one just twice as large as the other. Can you rearrange them (1) so as to enclose two four-sided spaces, one exactly three times as large as the other, and (2) so as to enclose two five-sided spaces, one exactly three times as large as the other? All the eighteen matches must be fairly used in each case; the two spaces must be quite detached, and there must be no loose ends or duplicated matches.

Solution